Debian-Projektleiterwahlen 2006

Zeitrahmen

Nominierungsperiode: 5. Februar, 00:00:01 UTC, 2006 26. Februar, 00:00:00 UTC, 2006
Wahlkampfperiode: 26. Februar, 00:00:01 UTC, 2006 19. März, 00:00:00 UTC, 2006
Abstimmungsperiode: 19. März, 00:00:01 UTC, 2006 9. April, 00:00:00 UTC, 2006

Bitte beachten Sie, dass die neue Amtszeit für den Projektleiter am 17. April 2006 beginnt.

Nominationen

  1. Jeroen van Wolffelaar [[email protected]] [Plattform]
  2. Ari Pollak [[email protected]] [Plattform]
  3. Steve McIntyre [[email protected]] [Plattform]
  4. Anthony Towns [[email protected]] [Plattform]
  5. Andreas Schuldei [[email protected]] [Plattform]
  6. Jonathan (Ted) Walther [[email protected]] [Plattform]
  7. Bill Allombert [[email protected]] [Plattform]

Der Stimmzettel kann via E-Mail mit Betreff leader2006 an [email protected] erhalten werden.

Debatte

Don Armstrong, David Nusinow, Thaddeus H. Black, Martin-Éric Racine und MJ Ray haben sich einverstanden erklärt, die Debatte zu moderieren. Ich möchte die Danksagungen des Projekts für ihre ausgezeichnete Arbeit bei der exzellent geleiteten Debatte und dem professionell dargestellten Rednerprotokoll aussprechen. Ein Mitschnitt der Debatte ist zur Begutachtung erhältlich.

Daten und Statistiken

Auch dieses Jahr werden – wie immer – Statistiken über die empfangenen Stimmzettel und verschickten Bestätigungen periodisch während des Wahlzeitraums gesammelt. Außerdem kann das Zähler-Blatt ebenfalls angesehen werden. Bitte denken Sie daran, dass die Wahl des Projektleiters einen geheimen Stimmzettel verwendet, so dass das Zähler-Blatt mit dem Hash des Wähler-Alias statt des Namens erstellt wird. Der Alias wurde dem entsprechenden Wähler mit der Bestätigung des Stimmzettels gemeinsam zugeschickt, so dass jeder überprüfen kann, dass die abgegebenen Stimmen korrekt sind. Während die Wahl lief, war das Zähler-Blatt ein Platzhalter; nach der Stimmabgabe wurde dort das endgültige Zähler-Blatt eingestellt. Bitte beachten Sie, dass die MD5-Summe für geheime Stimmzettel auf dem Platzhalter-Zähler-Blatt zufällig generiert wird, da andernfalls das Platzhalter-Zähler-Blatt Informationen in Bezug auf den MD5-Hash und den Wähler preisgeben würde.

Mindestanzahl

Mit 972 Entwicklern, haben wir: 

 Aktuelle Entwickler Anzahl = 972
 Q ( sqrt(#devel) / 2 )     = 15,5884572681199
 K min(5, Q )               = 5
 Quorum  (3 x Q )           = 46,7653718043597

Mehrheitsanforderung

Alle Kandidaten benötigen eine einfache Mehrheit, um geeignet zu sein.

Ergebnis

Der Gewinner der Wahl ist Anthony Towns

Ich möchte allen Kandidaten für ihre Arbeit am Projekt danken; dafür, dass sie sich für die Wahl zum Projektleiter zur Verfügung gestellt und den Entwicklern eine starke und brauchbare Gruppe von Kandidaten geboten haben.

Grafische Darstellung der Ergebnisse

Insgesamt abgegebene eindeutige Stimmen: 421, das sind 43,3127572% aller möglichen Stimmen.

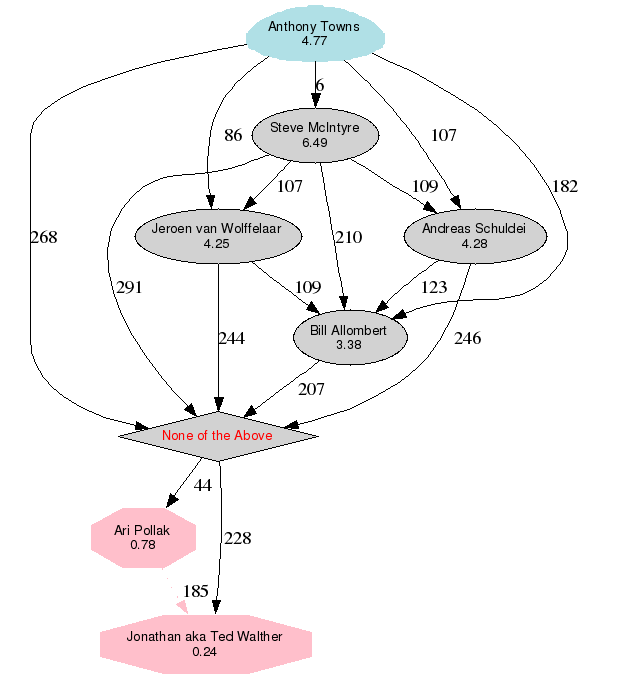
In der obigen Graphik implizieren die rosa gefärbte Knoten jene, die nicht die Mehrheit erlangten, der blaue ist der Gewinner. Das Achteck wird für die Optionen verwendet, die nicht den Standard geschlagen haben. In der folgenden Tabelle repräsentiert Anzahl[Zeile x][Spalte y] die Stimmen, die Option x über Option y erhalten hat. Vielleicht hilft eine detailliertere Erklärung der Ergebnismatrix beim Verständnis der Tabelle. Zum Verständnis der Condorcet-Methode ist der Wikipedia-Eintrag sehr informativ.

Die Ergebnismatrix
 Option
  1 2 3 4 5 6 7 8
Option 1   310 123 144 166 341 228 319
Option 2 40   34 46 45 246 48 158
Option 3 230 332   184 233 354 278 344
Option 4 230 334 190   242 365 281 339
Option 5 166 320 124 135   352 240 321
Option 6 20 61 16 16 16   21 73
Option 7 119 275 68 99 117 321   294
Option 8 75 202 53 71 75 301 87  

In Reihe 2, Spalte 1 sieht man, dass Ari Pollak
40 Stimmen über Jeroen van Wolffelaar erhalten hat.
In Reihe 1, Spalte 2 sieht man, dass Jeroen van Wolffelaar
310 Stimmen über Ari Pollak erhalten hat.

Paarweise Siege

Die Schwartz-Menge enthält

Der Gewinner

Debian benutzt die Condorcet-Methode für Wahlen. Vereinfachend kann die grundlegende Condorcet-Methode folgendermaßen beschrieben werden:
Ziehe alle möglichen Zweikämpfe zwischen den Kandidaten in Betracht. Der Condorcet-Gewinner, wenn es einen gibt, ist derjenige Kandidat, der jeden anderen Kandidaten im Zweikampf schlagen kann. Das Problem ist, dass es bei komplexen Wahlen durchaus zu einer kreisförmigen Beziehung kommen kann, in der A über B siegt, B über C siegt und C über A siegt. Die meisten Variationen von Condorcet verwenden verschiedene Mittel, um diese Pattsituation aufzulösen. Siehe Cloneproof Schwartz Sequential Dropping für Details. Die Variation von Debian ist in der Satzung schriftlich festgehalten, speziell § A.6.