Eleição do(a) líder do Projeto Debian 2006
Linha do tempo
| Período de candidatura: | 5 de fevereiro de 2006 00:00:01 UTC | 26 de fevereiro de 2006 00:00:00 UTC |
|---|---|---|
| Período de campanha: | 26 de fevereiro de 2006 00:00:01 UTC | 19 de março de 2006 00:00:00 UTC |
| Período de votação: | 19 de março de 2006 00:00:01 UTC | 9 de abril de 2006 00:00:00 UTC |
Por favor observe que o novo mandato do(a) líder do projeto deve começar em 17 de abril de 2006.
Candidaturas
- Jeroen van Wolffelaar [[email protected]] [plataforma]
- Ari Pollak [[email protected]] [plataforma]
- Steve McIntyre [[email protected]] [plataforma]
- Anthony Towns [[email protected]] [plataforma]
- Andreas Schuldei [[email protected]] [plataforma]
- Jonathan (Ted) Walther [[email protected]] [plataforma]
- Bill Allombert [[email protected]] [plataforma]
A cédula, pode ser recebida por e-mail, enviando uma mensagem [email protected] com o assunto leader2006.
Debate
Don Armstrong, David Nusinow, Thaddeus H. Black, Martin-Éric Racine, e MJ Ray concordaram em moderar o debate. Gostaria de extender os agradecimentos do projeto ao trabalho estrelar deles em conduzir um excelente debate orquestrado, e um log do debate renderizado profissionalmente. Uma transcrição do debate está disponível para revisão.
Dados e estatísticas
Esse ano, como sempre, serão coletadas estatísticas sobre as cédulas recebidas e os reconhecimentos enviados periodicamente durante o período de votação. Além disso, a lista de eleitores(as) será registrada. E também, o registro de contagem estará disponível para visualização. Por favor lembre-se de que a eleição do(a) líder do projeto tem uma cédula secreta, portanto, o registro de contagem será produzido com a hash do alias do(a) eleitor(a) ao invés do nome; o alias será enviado ao(à) eleitor(a) correspondente junto com o reconhecimento da cédula, para que a pessoa verifique se seu voto foi apurado corretamente. Enquanto a votação estiver aberta, o registro de contagem será fictício; após a votação, a registro de contagem final será disponibilizado. Por favor observe que, para as cédulas secretas, o md5sum no registro de contagem fictício é gerado aleatoriamente, caso contrário, o registro de contagem fictício vazaria informações relacionadas ao hash md5 e ao(a) eleitor(a).
Quorum
Com 972 desenvolvedores(as), temos:
Número atual de desenvolvedores = 972
Q ( raíz quadrada (núm. desenvolvedores) / 2 ) = 15.5884572681199
K min(5, Q ) = 5
Quorum (3 x Q ) = 46.7653718043597
Obs: Não usamos o formato "desenvolvedores(as)" para não gerar confusão com os parênteses da fórmula.
- Opção 1 alcançou o quorum: 319 > 47.0531614240744
- Opção 2 alcançou o quorum: 158 > 47.0531614240744
- Opção 3 alcançou o quorum: 344 > 47.0531614240744
- Opção 4 alcançou o quorum: 339 > 47.0531614240744
- Opção 5 alcançou o quorum: 321 > 47.0531614240744
- Opção 6 alcançou o quorum: 73 > 47.0531614240744
- Opção 7 alcançou o quorum: 294 > 47.0531614240744
Maioria requerida
Os(As) candidatos(as) precisam de maioria simples para serem elegíveis.
- A opção 1 supera a maioria. 4.253 (319/75) > 1
- A opção 2 foi retirada por não superar a maioria. 0.782 (158/202) <= 1
- A opção 3 supera a maioria. 6.491 (344/53) > 1
- A opção 4 supera a maioria. 4.775 (339/71) > 1
- A opção 5 supera a maioria. 4.280 (321/75) > 1
- A opção 6 foi retirada por não superar a maioria. 0.243 (73/301) <= 1
- A opção 7 supera a maioria. 3.379 (294/87) > 1
Resultado
O vencedor da eleição é Anthony Towns
Gostaria de agradecer a todos(as) os(as) candidatos(as) pelo serviço prestado ao projeto, por se candidatarem ao cargo de líder do projeto e por oferecer aos(às) desenvolvedores(as) um grupo forte e viável de candidatos(as).
Total de votos únicos depositados: 421, o que corresponde a 43,3127572% de todos os votos possíveis.
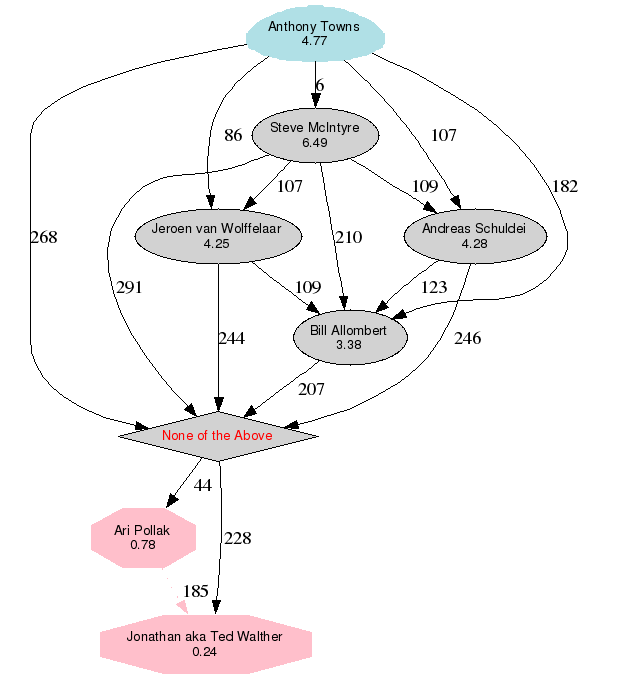
No gráfico acima, quaisquer nós de cor rosa implicam que a opção não superou a maioria, o azul é o vencedor. O octógono é usado para as opções que não superaram o padrão. Na tabela a seguir, o par[linha x][coluna y] representa os votos que a opção x recebeu sobre a opção y. Uma explicação mais detalhada da matriz de duelos pode ajudar na compreensão da tabela. Para entender o método de Condorcet, a página da Wikipedia é bastante informativa.
- Opção 1 "Jeroen van Wolffelaar"
- Opção 2 "Ari Pollak"
- Opção 3 "Steve McIntyre"
- Opção 4 "Anthony Towns"
- Opção 5 "Andreas Schuldei"
- Opção 6 "Jonathan aka Ted Walther"
- Opção 7 "Bill Allombert"
- Opção 8 "None of the Above (nenhuma das anteriores)"
| Opções | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Opção 1 | 310 | 123 | 144 | 166 | 341 | 228 | 319 | |
| Opção 2 | 40 | 34 | 46 | 45 | 246 | 48 | 158 | |
| Opção 3 | 230 | 332 | 184 | 233 | 354 | 278 | 344 | |
| Opção 4 | 230 | 334 | 190 | 242 | 365 | 281 | 339 | |
| Opção 5 | 166 | 320 | 124 | 135 | 352 | 240 | 321 | |
| Opção 6 | 20 | 61 | 16 | 16 | 16 | 21 | 73 | |
| Opção 7 | 119 | 275 | 68 | 99 | 117 | 321 | 294 | |
| Opção 8 | 75 | 202 | 53 | 71 | 75 | 301 | 87 | |
Olhando a linha 2, coluna 1, Ari Pollak
recebeu 40 votos sobre Jeroen van Wolffelaar
Olhando a linha 1, coluna 2, Jeroen van Wolffelaar
recebeu 310 votos sobre Ari Pollak.
Vitórias por pares
- Opção 3 vence a Opção 1 por ( 230 - 123) = 107 votos.
- Opção 4 vence a Opção 1 por ( 230 - 144) = 86 votos.
- Opção 1 vence a Opção 7 por ( 228 - 119) = 109 votos.
- Opção 1 vence a Opção 8 por ( 319 - 75) = 244 votos.
- Opção 4 vence a Opção 3 por ( 190 - 184) = 6 votos.
- Opção 3 vence a Opção 5 por ( 233 - 124) = 109 votos.
- Opção 3 vence a Opção 7 por ( 278 - 68) = 210 votos.
- Opção 3 vence a Opção 8 por ( 344 - 53) = 291 votos.
- Opção 4 vence a Opção 5 por ( 242 - 135) = 107 votos.
- Opção 4 vence a Opção 7 por ( 281 - 99) = 182 votos.
- Opção 4 vence a Opção 8 por ( 339 - 71) = 268 votos.
- Opção 5 vence a Opção 7 por ( 240 - 117) = 123 votos.
- Opção 5 vence a Opção 8 por ( 321 - 75) = 246 votos.
- Opção 7 vence a Opção 8 por ( 294 - 87) = 207 votos.
O conjunto de Schwartz contém
- Opção 4 "Anthony Towns"
Os(As) vencedores(as)
- Opção 4 "Anthony Towns"
O Debian usa o método de Condorcet para votação.
De forma simplista, o método de Condorcet puro
pode ser declarado da seguinte forma:
Considere todos os possíveis enfrentamentos entre pares de
candidatos(as).
O(A) vencedor(a) do Condorcet, se houver, é o(a)
candidato(a) que vencer cada um dos(as) outros(as)
candidatos(as) nesse enfrentamento por pares.
O problema é que, em eleições complexas, pode muito bem haver
uma relação circular em que A vence B, B vence C,
e C vence A. A maioria das variações no Condorcet usa vários
meios de resolver o empate. Veja
Cloneproof Schwartz Sequential Dropping (o método Schulze)
para mais detalhes. A variante do Debian é explicada na
constituição,
especificamente, § A.6.